12.3.2.1    CÁLCULO DE VIGAS.

 Ao acionarmos o calculo de vigas aparecerá a tela abaixo que mostra as opções da escolha da altura, verificações etc.

	Seleciona o piso que queremos efetuar o cálculo de vigas. Acima vemos a obra ativa.
	Numero da Viga Atual, Indicativo se está ou não detalhada e vão em metros do tramo selecionado..
	Vão ativo e geometria da seção da viga
	Opções de escolha da altura das vigas, h mínimo (altura mínima definida para o piso), 10% do vão (Normalmente não utilizada dá vigas muito altas), Flecha Máxima ( Sugere um h que respeita a flecha), Sub-Armação (Compressão somente suportada  pelo concreto isto é sem armadura dupla, vigas muito altas.)
	Valor do bw mínimo em cm , valor da altura míxima e define de que número a altura da viga é múltipla. Estes valores são obtidos inicialmente dos parâmetros da viga, porem você pode alterá-lo nesta própria tela para um valor valido para este calculo.
	Se acionado obedece o bw mínimo. e Extremos Semi Engastados os extremos das vigas passam a ser semi engastes e não mais apoio simples.
	Opções de verificação, com a sua devida tolerância obtida dos parâmetros da viga. Você pode selecionar quais parâmetros deseja ou não verificar, simplesmente marcando a opção com o mouse. Se houver alguma viga com erro o MultCalc NBR6118-V6 após a verificação estará posicionado na primeira viga com erro.
	Opções válidas para todas as vigas: Calcula todas as vigas deste piso, Aciona o Detalhamento de todas vigas, Recalcula todas ( Você recalcula vigas quando não quer perder o detalhamento anteriormente efetuado).
	Opções válidas para a viga ativa, Podemos alterar todos os vãos ou somente o vão ativo da viga Ativa. Podemos altera o Bw e o h de todas as vigas do piso, recalcular a viga ativa, Acionar o detalhamento da viga ativa

12.3.2.2    CÁLCULO E ALTERAÇÃO DAS VIGAS.

Após acionarmos o cálculo de vigas, aparecerá a informação de quantas vigas não atendem a verificação definida.

Para alterar a viga que não passou na verificação devemos primeira desativar todas as opções de escolha do H da viga, colocar o bw e h da nova seção e acionar os botões altera todos vãos e recalcula viga ativa. Se a nova seção atender a verificação definida o sistema mostrará menos uma viga com erros e ficará posicionado na próxima viga a ser alterada.

12.3.2.3    INFORMAÇÕES SOBRE ESFORÇOS CALCULADOS.

Vigas continuas segundo a NBR6118/2004

Os esforços nas armaduras podem ser considerados concentrados no centro de gravidade correspondente, se a distância deste centro ao ponto da seção de armadura mais afastada da linha neutra, medida normalmente a esta, for menor que 10% de h. As armaduras laterais de vigas podem ser consideradas no cálculo dos esforços resistentes, desde que estejam convenientemente ancoradas e emendadas.

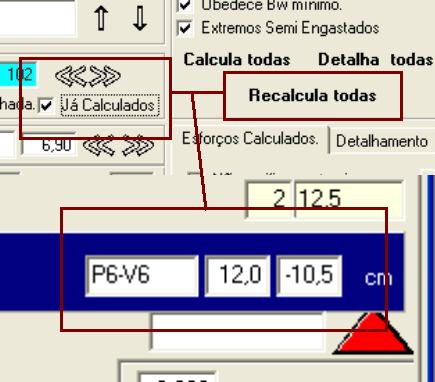
Na primeira passada de cálculo o sistema adota a largura dos pilares e das vigas como sendo iguais a largura da parede no osso ou 12 cm o que for maior, com estes dados dimensiona as vigas e passa os dados para o cálculo de pilares. Após o dimensionamento dos pilares já com as dimensões conhecidas devemos acionar a caixa mostrada acima [ já calculados] e acionarmos o botão Recalcula todas, com isto o sistema não altera as dimensões já definidas. O passo seguinte e detalhar as vigas para que as dimensões dos pilares e vigas fique representada em escala no desenho. Para projetos onde não haja pilares de extremidade com grandes dimensões não haverá grandes  reduções no tamanho do vão da viga e por conseguinte economia de estribos.

O Sistema calcula automaticamente a posição do pilar.

Verificação da fissuração segundo a NBR6118/2004

17.3.3 Estado limite de fissuração

17.3.3.1 Generalidades

Esta seção define os critérios para a verificação dos valores limites estabelecidos em 13.4 para a abertura de fissuras nos elementos estruturais lineares, analisados isoladamente e submetidos à combinação de ações conforme seção 11.

 17.3.3.2 Controle da fissuração através da limitação da abertura estimada das fissuras

O valor da abertura das fissuras pode sofrer a influência de restrições às variações volumétricas da estrutura, difíceis de serem consideradas nessa avaliação de forma suficientemente precisa. Além disso, essa abertura sofre também a influência das condições de execução da estrutura.

Por essas razões, os critérios apresentados a seguir devem ser encarados como avaliações aceitáveis do comportamento geral do elemento, mas não garantem avaliação precisa da abertura de uma fissura específica. Para cada elemento ou grupo de elementos das armaduras passiva e ativa aderente (excluindo-se os cabos protendidos que estejam dentro de bainhas), que controlam a fissuração do elemento estrutural, deve ser considerada uma área Acr do concreto de envolvimento, constituída por um retângulo cujos lados não distam mais de 7φ do contorno do elemento da armadura (ver figura 17.3). fluência

NOTA - É conveniente que toda a armadura de pele φi da viga, na sua zona tracionada, limite a abertura de fissuras na região Acri  correspondente, e que seja mantido um espaçamento menor ou igual a 15 φ.

A grandeza da abertura de fissuras, w, determinada para cada parte da região de envolvimento, é a menor entre as obtidas pelas expressões que seguem:

onde:

σsi, φi, Esi, ρri são definidos para cada área de envolvimento em exame.

Acri é a área da região de envolvimento protegida pela barra φi;

Esi é o módulo de elasticidade do aço da barra considerada, de diâmetro φi;

φi é o diâmetro da barra que protege a região de envolvimento considerada;

ρri é a taxa de armadura passiva ou ativa aderente (que não esteja dentro de bainha) em relação à área da região

de envolvimento (Acri);

σsi é a tensão de tração no centro de gravidade da armadura considerada, calculada no estádio II.

 Nos elementos estruturais com protensão, σsi é o acréscimo de tensão, no centro de gravidade da armadura, entre o estado limite de descompressão e o carregamento considerado. Deve ser calculado no estádio II, considerando toda a armadura ativa, inclusive aquela dentro de bainhas.

O cálculo no estádio II (que admite comportamento linear dos materiais e despreza a resistência à tração do

concreto) pode ser feito considerando a relação αe entre os módulos de elasticidade do aço e do concreto igual a 15.

η1 é o coeficiente de conformação superficial da armadura considerada, dado em 9.3.2.1 para passiva e substituído

por ηp1 para ativa, conforme 9.3.2.2. Nas vigas usuais, com altura menor que 1,2 m, pode-se considerar atendida a condição de abertura de fissuras em toda a pele tracionada, se a abertura de fissuras calculada na região das barras mais tracionadas for verificada e existir uma armadura lateral que atenda a 17.3.5.2.3.

ESTRIBOS

As seguintes prescrições são aplicáveis a elementos de comportamento unidimensional, sujeitos a esforços cortante e flexão combinados. O Modelo de Cálculo I admite a analogia com o modelo de treliça de banzos paralelos, cujas bielas de compressão assumem a inclinação constante ..=.45º (hipótese da treliça clássica), associada a mecanismos internos resistentes, correspondentes à parcela complementar Vc, supostamente inalterada para qualquer que seja esforço interno solicitante.

Dimensionamento da armadura transversal

O cálculo da armadura transversal pode ser obtido a partir da verificação do Estado Limite Último

Vsd força cortante solicitante de cálculo [N]

VRd3 força cortante resistente de cálculo, relativa à ruína pôr tração diagonal [N]

Vsw parcela da força cortante resistida pela armadura transversal [N]

Vc parcela da força cortante absorvida pelos mecanismos internos [N]

Particularizando-se para  estribos verticais (a.=.90)

VERIFICAÇÕES

Verificação da armadura transversal mínima

Verificação do espaçamento longitudinal e transversal máximos

Verificação do esmagamento das bielas de concreto

Armadura de pele

Viga Te

14.6.2.2 Largura colaborante de vigas de seção T

Quando a estrutura for modelada sem a consideração automática da ação conjunta de lajes e vigas, esse efeito pode ser considerado mediante a adoção de uma largura colaborante da laje associada à viga, compondo uma seção transversal T.

A consideração da seção T pode ser feita para estabelecer as distribuições de esforços internos, tensões, deformações e deslocamentos na estrutura, de uma forma mais realista. A largura colaborante bf deve ser dada pela largura da viga bw acrescida de no máximo 10% da distância a entre pontos de momento fletor nulo, para cada lado da viga em que houver laje colaborante. A distância a pode ser estimada, em função do comprimento l do tramo considerado, como se apresenta a seguir:

- viga simplesmente apoiada: a = 1,00 l

Formulário flecha imediata 

Segundo a NB6118/2004

Espaçamento dos ferros em função do agregado, bitolas e diâmetro do vibrador.

Define-se comprimento de ancoragem básico como o comprimento reto de uma barra de armadura passiva necessário para ancorar a força limite Asfyd nessa barra, admitindo, ao longo desse comprimento, resistência de aderência uniforme e igual a fbd, conforme 9.3.2.1.

O comprimento de ancoragem básico é dado por:

9.4.2.5 Comprimento de ancoragem necessário

O comprimento de ancoragem necessário pode ser calculado por:

12.3.2.4    JANELA DE ESFORÇOS CALCULADOS.

Vamos descrever passo a passo todos os itens mostrados acima:

Controle da fissuração será 2 mm se estiver acionado concreto protendido, e 3 mm se estiver selecionado concreto armado. Para o nosso caso dever ser 3 mm.

Momentos Nos apoios

A esquerda é mostrado o momento a esquerda do vão em Tcm, na linha de baixo a área de ferro necessária (qdo for armadura dupla o segundo campo será diferente de 0,00). Na ultima linha a quantidade de ferros e a bitola da parte superior da armadura, a dupla só será conhecida no detalhamento pois dependendo do que tem na parte inferior da viga. As informações da direita são referentes ao apoio direto. No centro é mostrado o vão ativo e as dimensões do vão em metros.

Reação nos apoios e Momento no vão.

A esquerda é mostrado o cortante em Toneladas, a área de ferro necessária e na ultima linha o detalhamento bitola e estribos por metro. A direita as informações do cortante a direita . No centro é mostrado o momento no vão e Tcm a armadura necessária e o detalhamento dos ferros, o detalhamento otimizado só será mostrado na janela de detalhamento.

Cortantes Máximos e Mínimos da seção.

Flecha diferida levando em conta o carregamento permanente P + 0,3 Q, w=03 NB1/2004  edifícios residenciais, valor limite para efeitos visuais e na linha de baixo a flecha levando-se em conta somente as cargas Acidentais e ao lado o máximo permitido para o efeito de vibração. Na esquerda e mostrado em vermelho o limite de contra flecha permitido pela norma e uma caixa onde podemos selecionar se resolveremos o problema de flecha com contra flecha ou com o aumento da seção. Na parte inferior e mostrado: O campo flecha não está mais em vermelho indicando que com a contra flecha o limite visual é solucionado , Para aceitar esta solução acione a caixa

Escalas para desenho a primeira é a escaha Horizontal e a segunda a escala vertical. Na esquerda vemos o campo desvio do eixo + - (cm), que indica o deslocamento do centro da viga para a esquerda ou direita da parede de referencia, é útil para o caso de vigas de extremidade mais largas que a parede e para requadrar as vigas mais largas que as paredes para peças menos nobres.

Caixa marca a viga como ok, mesmo com mensagem de erro, serve para o caso de resolver a flecha com contra flecha ou para aceitar vigas com mensagem de fissuração ou outra verificação a critério e responsabilidade do calculista.  Informa se a viga transmitirá torção de apoio para a viga suporte. Permite alterar este dado na viga que está sendo calculada. Botão Salva, torna efetivo toda a alteração efetuada em cada vão, portanto após alterar algo em um vão acione o botão salva.

Dimensões e posição apoios.

Quando estiver selecionado ao recalcular a viga o sistema obtêm automaticamente a dimensão do pilar e a sua posição relativa. Caso você discorde do valor obtido altere e acione o botão Salva

12.3.2.5    JANELA DE DETALHAMENTO.

12.3.2.6    JANELA DO CARREGAMENTO DA VIGA.

Na dados de carregamento podemos ter até 10 conjuntos de cargas por vão, As corres definem a correlação entre dados e desenho. Carga concentrada no fim do conjunto de carga, na carga distribuída não aparece o peso próprio que é computado na hora do cálculo para utilizar o valor mais correto. e a extensão que indica o tamanho da carga.

Quando tiver um pilar nascendo em cima da viga, as esperas são detalhadas automaticamente, caso você deseje eliminar o detalhamento desta espera acione a caixa não detalha esperas. Quando na viga houver mudança de direção automaticamente será levada em conta o momento torsor devido a carga concentrada (amarelo x azul) e a carga distribuída (marrom x verde). Em alguns casos por ex. quando ha rigidez da laje é suficiente para resistir ao torcionamento da viga você pode acionar desligar  a caixa Considera esta Torção, neste caso a torção será resistida pela laje. O botão salva que quando acionado salva definitivamente as alterações efetuadas no vão selecionado.

12.3.2.7    JANELA DA MEMÓRIA DE CALCULO.

São mostrados os dados que foram considerados na viga e os valores indicando momentos, áreas de ferros, posições dos momentos máximos e posições dos momentos nulos etc.

12.3.2.8    JANELA DA REAÇÃO NOS PILARES.

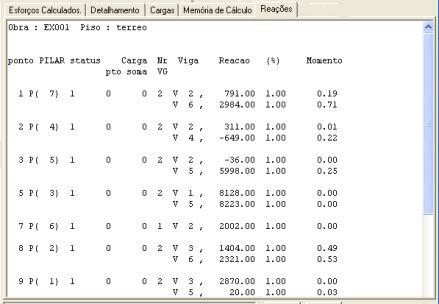
Mostra para cada pilar, quantas e quais vigas chegam nele, e com que carregamento e momento elas contribuem para o carregamento do pilar.

12.3.2.9    JANELA DE GERAÇÃO DO DESENHO.

Erro tolerado para escolha de As

Área de ferro das bitolas em milímetro iguais a bitola em polegadas da bitola compatível.

	O sistema escolhe o a menor bitola para utilizar como porta estribo, porem você poderá alterar para outro de sua escolha. Nível de referência do piso e uma caixa indicando sua colocação no desenho.
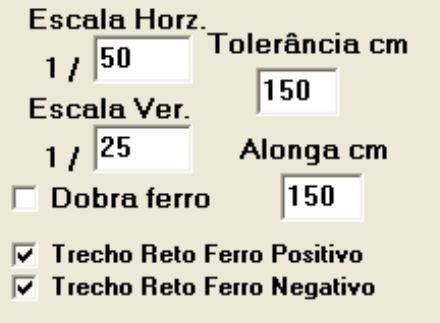	Permite alterar a escala Horizontal e Vertical do detalhamento. Tolerância em cm indica a partir de que distância o sistema pode unir dois ferros de mesma bitola para simplificar o detalhamento. Alonga cm informa para o sistema qual a distância do apoio do ferro negativo que pode ser alongada até o apoio para simplificar o detalhamento. Dobra ferro permite que o sistema dobre o ferro positivo após o cobrimento do diagrama para ajudar no combate ao cisalhamento. Coloca ou não a dimensão dos trechos retos do ferro positivo e ou negativo.
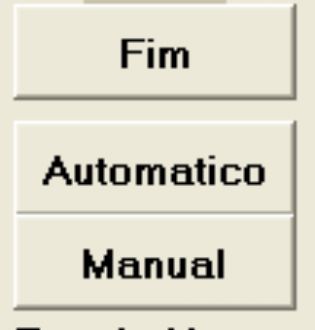	Fim , termina a escolha de ferros e volta para a tela de calculo. Automático, o sistema escolhe automaticamente as bitolas dos ferros. Manual, será apresentada as opções e engenheiro seleciona a que quer usar. Veja abaixo a opção manual.

Na primeira opção desenho da viga fica no topo do papel, e na segunda o espaço entre o desenho dos ferros fica menor.

CÁLCULOS