|
|
|
|
|
|
MultCalc NBR6118-V6 (c) HighSolution 2006 |
|
|
|
|
|
12.3.3.1 CÁLCULO DE PILARES.
Ao acionarmos o calculo de pilares aparecerá a tela abaixo que mostra as opções da escolha das dimensões , verificações etc.
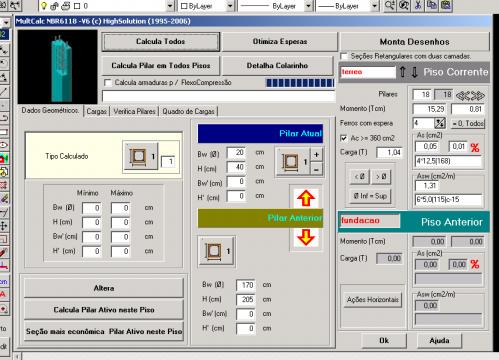
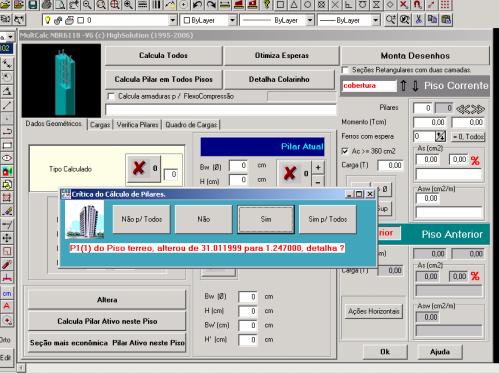
Sempre que ha alteração na carga dos pilares o sistema pergunta se é para detalhar o pilar novamente.
 |
Se este item estiver desmarcado, o pilar será calculado com o método pilar padrão com curvatura aproximada, Se este item estiver selecionado será calculado como flexo compressão. (veja detalhe no próximo quadro) |
 |
Qdo no item acima estiver selecionado Flexo-compressão você poderá optar pelo método geral ou escolher que a armadura da seção retangular seja otimizada em somente 2 camadas. |
 |
Seleciona o piso que queremos efetuar o cálculo de lajes. Acima vemos a obra ativa. |
 |
Numero do Pilar Atual |
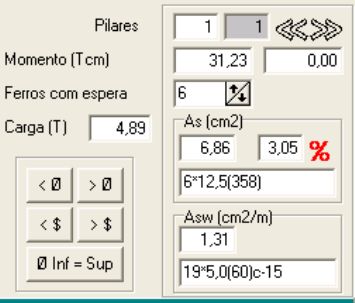 |
Dados do pilar atual, Momento em Tcm nas direções x e y. Carga em Toneladas. Armadura calculada e percentual da armadura. Estribo calculado. O botão com o símbolo de bitola permite aumentar ou diminuir a bitola escolhida. O botão fi inferior igual a fi superior permite que se faça que o pilar de baixo fique com o mesmo número de ferros que o de cima. |
|
|
Mostra as dimensões do Pilar Atual e do Pilar do Piso Anterior |
|
|
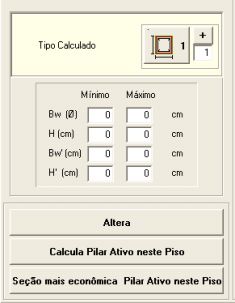
Mostra o Tipo do pilar Calculado. As Dimensões mínimas selecionadas para este Pilar. O botão que permite Alterar os dados deste pilar. O botão que aciona o cálculo deste pilar neste piso. O botão que permite selecionar a seção mais econômica para este pilar. |
|
|
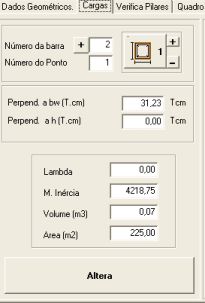
Na aba Cargas é mostrado: O número da barra e do ponto que o pilar esta situado. O momento perpendicular a bw e o momento perpendicular a h. em (Tcm) Valores característicos da seção como por ex: Inércia, Volume e Area. botão altera que permite salvar qualquer alteração executada. |
|
|
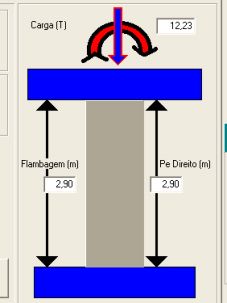
Esquemático das cargas atuantes no pilar, com o seu pé direito e altura do comprimento de flambagem. |
|
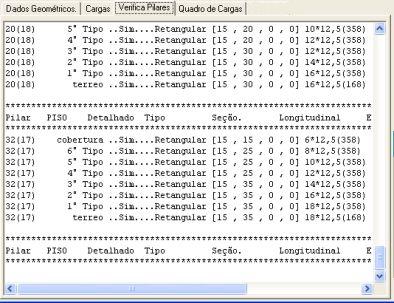
Relatório de verificação do calculo dos pilares. |
|
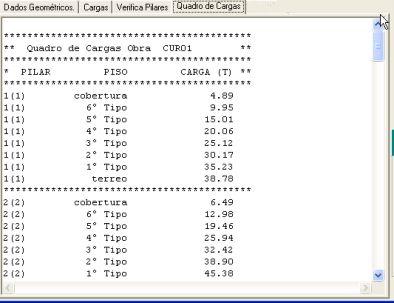
Quadro de cargas da obra |
12.3.3.2 CÁLCULO E ALTERAÇÃO DOS PILARES.
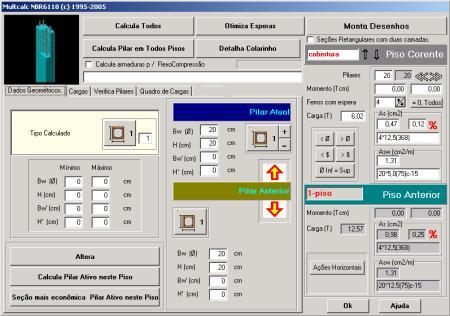
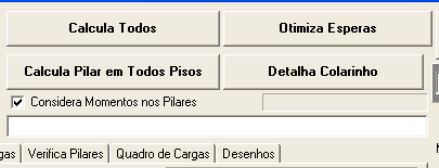
Poderemos adicionalmente quando for conveniente desconsiderar os momentos externos nos pilares.
Após posicionarmos o Pilar atual no primeiro pilar do piso mais acima do projeto, Acionamos o botão Calcula todos que calculara todos os pilares em todos os pisos (ficando somente para detalhar o colarinho).
Uma segunda opção e solicitarmos que o sistema calcule o pilar ativo em todos os pisos.
Após o calculo dos pilares deveremos acionar o relatório de verificação e estando tudo ok, passaremos para o detalhamento do colarinho que resulta numa seção sempre que possível igual a superior e com o mesmo número de ferros. Acionamos o relatório de verificação novamente e se ok passaremos para otimização das esperas.
Na otimização das esperas o sistema elimina as esperas que não são necessárias no piso superior.
12.3.3.3 INFORMAÇÕES SOBRE ESFORÇOS CALCULADOS.
NBR6118/2004
Efeitos de 2a ordem são aqueles que
2a ordem localizados15.4.2 Estruturas de nós fixos e estruturas de nós moveis
As estruturas são consideradas, para efeito de cálculo, como de nós fixos, quando os deslocamentos horizontais dos nós são pequenos e, por decorrência, os efeitos globais de 2a ordem são desprezíveis (inferiores a 10% dos respectivos esforços de 1a ordem). Nessas estruturas, basta considerar os efeitos locais e localizados de 2a ordem. As estruturas de nós móveis são aquelas onde os deslocamentos horizontais não são pequenos e, em decorrência, os efeitos globais de 2a ordem são importantes (superiores a 10% dos respectivos esforços de 1a ordem). Nessas estruturas devem ser considerados tanto os esforços de 2a ordem globais como os locais e localizados.
Todavia, há estruturas em que os deslocamentos horizontais são grandes e que, não obstante, dispensam a consideração dos efeitos de 2a ordem por serem pequenas as forças normais e, portanto, pequenos os acréscimos dos deslocamentos produzidos por elas; isso pode acontecer, por exemplo, em postes e em certos pilares de galpões industriais.
"As deformações existentes na estruturas permitem calcular os efeitos de Segunda ordem que de acordo com o item 15.4.1 podem ser divididos em Efeitos Globais e Locais e Localizadas de Segunda Ordem. Sob a ação das cargas verticais e horizontais, os nós da estrutura deslocam-se horizontalmente.
Os esforços de segunda ordem decorrentes desses deslocamentos são chamados efeitos globais de 2ª ordem. Nas barras da estrutura, os respectivos eixos não se mantêm retilíneos, surgindo aí efeitos locais de 2ª ordem que, em princípio, afetam principalmente os esforços solicitantes ao longo delas. Em pilares parede (simples ou compostos) pode-se ter uma região que apresenta não retilineidade maior do que a do pilar como um todo. Nestas regiões surgem efeitos de 2ª ordem maiores, chamados de efeito de 2ª ordem localizados. O efeito de 2ª ordem localizado além de aumentar nesta região a flexão longitudinal, aumenta também a flexão transversal, havendo a necessidade de aumentar os estribos nestas regiões.
Na figura 1 estão representadas as possibilidades de instabilidade que podem ser causadas por cada uma das duas primeiras situações.
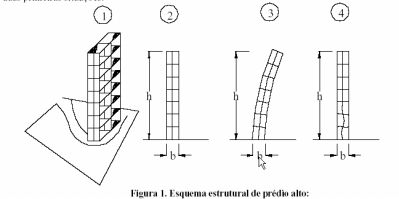
1) perspectiva esquemática; 2) estrutura vertical indeformada; 3) edificação sujeita a instabilidade global; 4) instabilidade local de pilares centrais inferiores
Teoricamente todas as três situações descritas anteriormente devem ser verificadas e, preferencialmente, considerando a não linearidade geométrica e física do material e considerando o comportamento tridimensional da estrutura. É fácil perceber a dificuldade na realização de um cálculo deste, e assim é comum separar os problemas e verificar inicialmente a estabilidade global, a local e finalmente a localizada. Na sequência será estudada apenas a estabilidade global, ficando a local para quando forem abordados os pilares de edifícios.
"(PILARES DE CONCRETO ARMADO ROBERTO CHUST CARVALHO / JASSON R. FIGUEIREDO FILHO).
15.4.3 Contraventamento
Por conveniência de análise, é possível identificar, dentro da estrutura, subestruturas que, devido à sua grande rigidez a ações horizontais, resistem à maior parte dos esforços decorrentes dessas ações. Essas subestruturas são chamadas subestruturas de contraventamento. Os elementos que não participam da subestrutura de contraventamento são chamados elementos contraventados. As sub-estruturas de contraventamento podem ser de nós fixos ou de nós moveis, de acordo com as definições de 15.4.2.
15.4.4 Elementos isolados
São considerados elementos isolados os seguintes:
a) os elementos estruturais isostáticos;
b) os elementos contraventados;
c) os elementos das estruturas de contraventamento de nós fixos;
d) os elementos das subestruturas de contraventamento de nós moveis desde que, aos esforços nas extremidades, obtidos numa análise de 1a ordem, sejam acrescentados os determinados por análise global de 2a ordem.
15.5 Dispensa da consideração dos esforços globais de 2a ordem
15.5.1 Generalidades
Os processos aproximados, apresentados em 15.5.2 e 15.5.3, podem ser utilizados para verificar a possibilidade de dispensa da consideração dos esforços globais de 2a ordem, ou seja, para indicar se a estrutura pode ser classificada como de nós fixos, sem necessidade de cálculo rigoroso.
15.5.2 Parâmetro de instabilidade
Uma estrutura reticulada simétrica pode ser considerada como sendo de nós fixos se seu parâmetro de instabilidade α for menor que o valor α1, conforme a expressão:
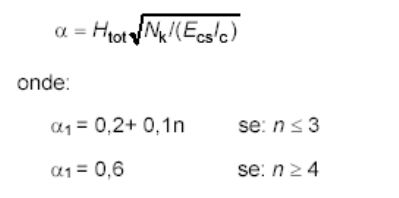
onde:
n é o número de níveis de barras horizontais (andares) acima da fundação ou de um nível pouco deslocável do subsolo;
Htot é a altura total da estrutura, medida a partir do topo da fundação ou de um nível pouco deslocável do subsolo;
Nk é a somatória de todas as cargas verticais atuantes na estrutura (a partir do nível considerado para o cálculo de Htot), com seu valor característico;
EcsIc representa a somatória dos valores de rigidez de todos os pilares na direção considerada. No caso de estruturas de pórticos, de treliças ou mistas, ou com pilares de rigidez variável ao longo da altura, pode ser considerado o valor da expressão EcsIc de um pilar equivalente de seção constante.
NOTA - Na análise de estabilidade global pode ser adotado o valor do módulo de elasticidade ou módulo de deformação tangente inicial dado em 8.2.8.
O valor de Ic deve ser calculado considerando as seções brutas dos pilares. A rigidez do pilar equivalente deve ser determinada da seguinte forma: . calcular o deslocamento do topo da estrutura de contraventamento, sob a ação do carregamento horizontal;. calcular a rigidez de um pilar equivalente de seção constante, engastado na base e livre no topo, de mesma altura Htot , tal que, sob a ação do mesmo carregamento, sofra o mesmo deslocamento no topo.
O valor limite α1 = 0,6 prescrito para n . 4 é, em geral, aplicável às estruturas usuais de edifícios. Pode ser adotado para associações de pilares-parede e para pórticos associados a pilares-parede. Pode ser aumentado para α1 = 0,7 no caso de contraventamento constituído exclusivamente por pilares-parede e deve ser reduzido para α1 = 0,5 quando só houver pórticos.
15.5.3 Coeficiente γz
O coeficiente γz de avaliação da importância dos esforços de segunda ordem global é válido para estruturas reticuladas de no mínimo quatro andares. Ele pode ser determinado a partir dos resultados de uma análise linear de primeira ordem, para cada caso de carregamento, adotando-se os valores de rigidez dados em 15.7.2.
O valor de γz para cada combinação de carregamento é dado pela expressão:
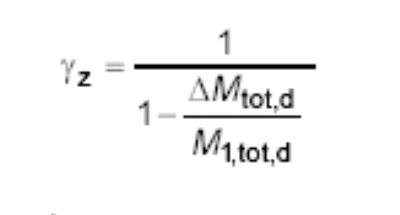
onde:
M1,tot,d é o momento de tombamento, ou seja, a soma dos momentos de todas as forças horizontais da combinação considerada, com seus valores de cálculo, em relação à base da estrutura;
.Mtot,d é a soma dos produtos de todas as forças verticais atuantes na estrutura, na combinação considerada, com seus valores de cálculo, pelos deslocamentos horizontais de seus respectivos pontos de aplicação, obtidos da análise de 1a ordem;
Considera-se que a estrutura é de nós fixos se for obedecida a condição: γz <= 1,1.
15.6 Análise de estruturas de nós fixos
Nas estruturas de nós fixos, o cálculo pode ser realizado considerando cada elemento comprimido isoladamente, como barra vinculada nas extremidades aos demais elementos estruturais que ali concorrem, onde se aplicam os esforços obtidos pela análise da estrutura efetuada segundo a teoria de 1a ordem.
A análise dos efeitos locais de 2a ordem deve ser realizada de acordo com o estabelecido em 15.8.
Sob a ação de forças horizontais, a estrutura é sempre calculada como deslocável. O fato de a estrutura ser classificada como sendo de nós fixos dispensa apenas a consideração dos esforços globais de 2a ordem.
O comprimento equivalente le do elemento comprimido (pilar), suposto vinculado em ambas as extremidades, deve ser o menor dos seguintes valores:
le = l0 + h
le = l
onde:
l0 é a distância entre as faces internas dos elementos estruturais, supostos horizontais, que vinculam o pilar;
h é a altura da seção transversal do pilar, medida no plano da estrutura em estudo;
l é a distância entre os eixos dos elementos estruturais aos quais o pilar está vinculado.
15.7 Análise de estruturas de nós móveis
15.7.1 Generalidades
Na análise estrutural de estruturas de nós móveis devem ser obrigatoriamente considerados os efeitos da não linearidade geométrica e da não linearidade física e, portanto, no dimensionamento devem ser obrigatoriamente considerados os efeitos globais e locais de 2a ordem.
15.7.2 Análise não-linear com 2a ordem
Uma solução aproximada para a determinação dos esforços globais de 2a ordem consiste na avaliação dos esforços finais (1a ordem + 2a ordem) a partir da majoração adicional dos esforços horizontais da combinação de carregamento considerada por 0,95γz. Esse processo só é válido para γz <= 1,3.
15.7.3 Consideração aproximada da não-linearidade física
Para a análise dos esforços globais de 2a ordem, em estruturas reticuladas com no mínimo quatro andares, pode ser considerada a não-linearidade física de maneira aproximada, tomando-se como rigidez dos elementos estruturais os valores seguintes:
- lajes: (EI)sec= 0,3EciIc
- vigas: (EI)sec= 0,4EciIc para As’ <> As e
(EI)sec = 0,5 EciIc para As’ = As
- pilares: (EI)sec=0,8EciIc
onde:
Ic é o momento de inércia da seção bruta de concreto, incluindo, quando for o caso, as mesas colaborantes.
Quando a estrutura de contraventamento for composta exclusivamente por vigas e pilares e γz for menor que 1,3, permite-se calcular a rigidez das vigas e pilares por: (EI)sec = 0,7 EciIc
Os valores de rigidez adotados nesta subseção são aproximados e não podem ser usados para avaliar esforços locais de 2a ordem, mesmo com uma discretização maior da modelagem.
15.7.4 Análise dos efeitos locais de 2ª ordem
A análise global de 2a ordem fornece apenas os esforços nas extremidades das barras, devendo ser realizada uma análise dos efeitos locais de 2a ordem ao longo dos eixos das barras comprimidas, de acordo com o prescrito em 15.8.
Os elementos isolados, para fins de verificação local, devem ser formados pelas barras comprimidas retiradas da estrutura, com comprimento le, de acordo com o estabelecido em 15.6, porém aplicando-se às suas extremidades
os esforços obtidos através da análise global de 2a ordem.
15.8 Análise de elementos isolados
15.8.1 Generalidades
As subseções 15.8.2, 15.8.3.2. e 15.8.4 são aplicáveis apenas a elementos isolados de seção constante e armadura constante ao longo de seu eixo, submetidos à flexo-compressão.
Os pilares devem ter índice de esbeltez menor ou igual a 200 (λ <= 200). Apenas no caso de postes com força normal
menor que 0,10 fcd Ac, o índice de esbeltez pode ser maior que 200.
15.8.2 Dispensa da análise dos efeitos locais de 2a ordem
Os esforços locais de 2a ordem em elementos isolados podem ser desprezados quando o índice de esbeltez for menor que o valor limite λ1 estabelecido nesta subseção.
O índice de esbeltez deve ser calculado pela expressão: λ = e l /i
No caso de pilar engastado na base e livre no topo, o valor de e l é igual a 2 l . Nos demais casos, adotar os valores calculados conforme 15.6.
O valor de λ1 depende de diversos fatores, mas os preponderantes são:
- a excentricidade relativa de 1a ordem e1/h;
- a vinculação dos extremos da coluna isolada;
- a forma do diagrama de momentos de 1a ordem.
O valor de λ1 pode ser calculado pela expressão:

onde: MA e MB são os momentos de 1a ordem nos extremos do pilar. Deve ser adotado para MA o maior valor absoluto ao longo do pilar biapoiado e para MB o sinal positivo, se tracionar a mesma face que MA, e negativo, em caso contrário.
b) para pilares biapoiados com cargas transversais significativas ao longo da altura:

O momento MA é o momento de 1a ordem no engaste e MC é o momento de 1a ordem no meio do pilar embalanço.
d) para pilares biapoiados ou em balanço com momentos menores que o momento mínimo estabelecido em 11.3.3.4.3:
αb = 1,0
15.8.3 Determinação dos efeitos locais de 2a ordem
15.8.3.1 Barras submetidas a flexo-compressão normal
O cálculo pode ser feito pelo método geral ou por métodos aproximados, de acordo com 15.8.3.2 ou 15.8.3.3.
A consideração da fluência é obrigatória para λ > 90, devendo ser acrescentada a M1d a parcela correspondente à excentricidade ecc definida em 15.8.4.
15.8.3.2 Método geral
Consiste na análise não-linear de 2a ordem efetuada com discretização adequada da barra, consideração da relação momento-curvatura real em cada seção, e consideração da não-linearidade geométrica de maneira não aproximada.
O método geral é obrigatório para λ >140.
15.8.3.3 Métodos aproximados
15.8.3.3.1 Generalidades
A determinação dos esforços locais de 2ª ordem pode ser feita por métodos aproximados como o do pilar padrão e o do pilar-padrão melhorado.
15.8.3.3.2 Método do pilar-padrão com curvatura aproximada
Pode ser empregado apenas no cálculo de pilares com λ = 90, seção constante e armadura simétrica e constante ao longo de seu eixo. A não-linearidade geométrica é considerada de forma aproximada, supondo-se que a deformação da barra seja senoidal.
A não-linearidade física é considerada através de uma expressão aproximada da curvatura na seção crítica.
O momento total máximo no pilar deve ser calculado pela expressão:

onde:
h é a altura da seção na direção considerada;
ν é a força normal adimensional;
M1d,min tem o significado e o valor estabelecidos em 11.3.3.4.3.
O momento M1d,A e o coeficiente αb têm as mesmas definições de 15.8.2, sendo M1d,A o valor de cálculo de 1a ordem do momento MA.
15.8.3.3.3 Método do pilar-padrão com rigidez κ aproximada
Pode ser empregado apenas no cálculo de pilares com λ = 90, seção retangular constante, armadura simétrica e constante ao longo de seu eixo.
A não-linearidade geométrica deve ser considerada de forma aproximada, supondo-se que a deformação da barra seja senoidal.
A não linearidade física deve ser considerada através de uma expressão aproximada da rigidez.
O momento total máximo no pilar deve ser calculado pela expressão:
O momento total máximo no pilar deve ser calculado a partir da majoração do momento de 1a ordem pela expressão:
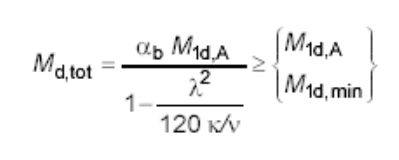
sendo o valor da rigidez adimensional κ dado aproximadamente pela expressão:
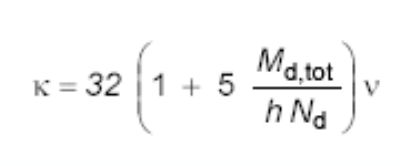
As variáveis h, ν, M1d,A e αb são as mesmas definidas na subseção anterior. Usualmente duas ou três iterações são suficientes quando se optar por um cálculo iterativo.
15.8.3.3.4 Método do pilar-padrão acoplado a diagramas M, N , 1/r
A determinação dos esforços locais de 2a ordem em pilares com λ <= 140 pode ser feita pelo método do pilar-padrão ou pilar-padrão melhorado, utilizando-se para a curvatura da seção crítica valores obtidos de diagramas M, N, 1/r específicos para o caso.
Se λ > 90, é obrigatória a consideração dos efeitos da fluência, de acordo com 15.8.4.
15.8.3.3.5 Método do pilar-padrão para pilares da seção retangular submetidos à flexão composta oblíqua
Quando a esbeltez de um pilar de seção retangular submetido à flexão composta oblíqua for menor que 90 (λ < 90) nas duas direções principais, pode ser aplicado o processo aproximado descrito em 15.8.3.3.3 simultaneamente em cada uma das duas direções.
A amplificação dos momentos de 1a ordem em cada direção é diferente, pois depende de valores distintos de rigidez e esbeltez.
Uma vez obtida a distribuição de momentos totais, de 1a e 2a ordem, em cada direção, deve ser verificada, para cada seção ao longo do eixo, se a composição desses momentos solicitantes fica dentro da envoltória de momentos resistentes para a armadura escolhida. Essa verificação pode ser realizada em apenas três seções: nas extremidades A e B e num ponto intermediário onde se admite atuar concomitantemente os momentos Md,tot nas duas direções (x e y).
15.8.4 Consideração da fluência
A consideração da fluência deve obrigatoriamente ser realizada em pilares com índice de esbeltez λ > 90 e pode ser efetuada de maneira aproximada, considerando a excentricidade adicional ecc dada a seguir:

A consideração do efeito de 2a ordem deve ser feita conforme 15.8.3, como se fosse um efeito imediato, que se soma à excentricidade e1.
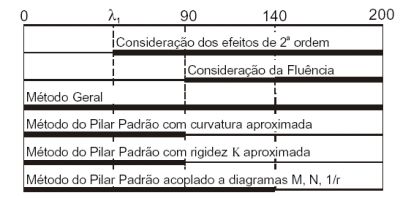
Calculo de pilares , Critérios para modelagem em função do índice de esbeltez.
12.3.3.4 Montagem dos desenhos.
Você poderá ver o detalhamento do Pilar com a posição dele na estrutura.