Em problemas reais, as condições de apoio das lajes diferem das que acaba-mos de discutir nos posts anteriores.
Regra geral, estes elementos estruturais apoiam-se em elementos deformá-veis (vigas, pilares, paredes de rigidez finita), pelo que as condições de fronteira deverão ser alteradas para ter em conta este efeito do apoio ser elástico.

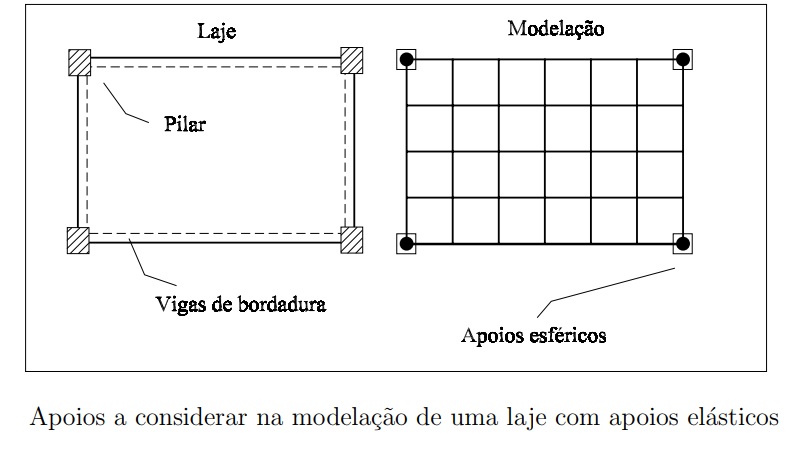
Considere-se por exemplo a laje retangular representada na figura acima, onde se assume a existência de uma viga de bordadura de rigidez aflexãoo EIv e uma rigidez a torção dada por GJv. Considere-se ainda que o sistema laje + vigas de bordadura descarrega em quatro pilares localizados nos vértices da laje.
Se se assumisse que os bordos se encontram simplesmente apoiados, as condições de fronteira seriam as habituais, ou seja w = 0 ; mn = 0

Neste caso, apenas se poder´a dizer que Wlaje = Wviga e Mnlaje = Tviga
onde Wviga e Tviga representam o campo de deslocamentos transversais e o campo de momentos torsores na viga, respectivamente.
Os únicos apoios a considerar são os apoios elásticos representados na modelagem apresentada a direita da figura acima. Esses apoios devem restringir apenas o deslocamento transversal e a sua rigidez deve ser dada pela rigidez axial dos pilares considerados.
Para se conseguir modelar o comportamento conjunto da laje e das vigas de bordas, deve ter-se em conta que nas barras dispostas ao longo da fronteira se devem considerar em simultâneo as propriedades geométricas e elásticas envolvidas na caracterização da faixa de laje correspondente e as propriedades necessárias à caracterização das vigas das bordas propriamente ditas.
Desta forma, deverá considerar-se para esses elementos da discretização:

Modelagem mais real das condições de apoio de lajes, apoios deformáveis (Vigas, Pilares, Paredes com rigidez finita).