Análise de uma laje em L
Ilustra-se nesta post a aplicação da técnica de modelagem na análise de uma laje com geometria e condições de apoio mais gerais do que as que foram consideradas no post anterior.
Considera-se para tal efeito a laje em L representada na figura abaixo, na qual existem bordos engastados, simplesmente apoiados e livres. No canto entre os dois bordos livres considera-se ainda a existência de um pilar.
A laje tem uma espessura de 0, 20 m e continua a assumir-se para o material estrutural um módulo de elasticidade de E = 30500000 kN/m2 e um coeficiente de Poisson ν = 0, 2. Considera-se que está aplicada em toda a laje uma carga uniformemente distribuída com um valor de 10 kN/m2.
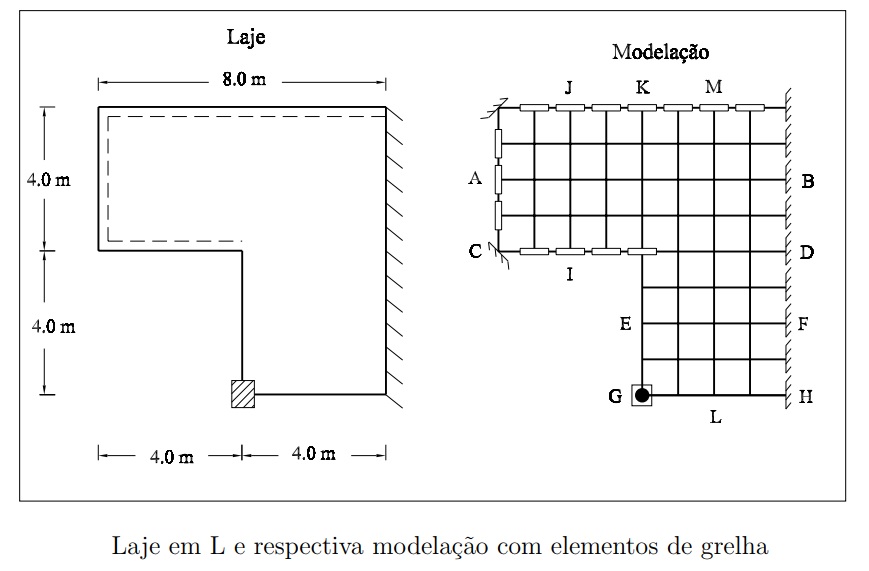
A modelagem considerada na análise da laje. Sendo o espaçamento entre barras unitário (1 metro) , o valor da rigidez a flexão e da rigidez a torção nas barras com bw 0,5 metros Ieq = 0,00034722 m4 e Jeq = 0,0006666 m4. para as barras com bw 1,0 metro Ieq = 0,00069444 m4 e Jeq = 0,0013333 m4.
Nos nós interiores são aplicadas cargas verticais concentradas com valores dados por Fv = 10 × 1, 0 × 1, 0 = 10kN . Para os nós existentes sobre os bordos livres, a respectiva área de influência é diferente, pelo que o valor das cargas concentradas a aplicar nestes casos vem agora dado por Fbordo = 10 × 0, 5 × 1, 0 = 5kN . Nos nós existentes sobre os
bordos engastados, apoiados e sobre o pilar não é necessário definir qualquer carregamento, como já aconteceu no post anterior. Os bordos apoiados foram modelados com apoio cilíndrico, e o pilar foi considerado um apoio esférico.


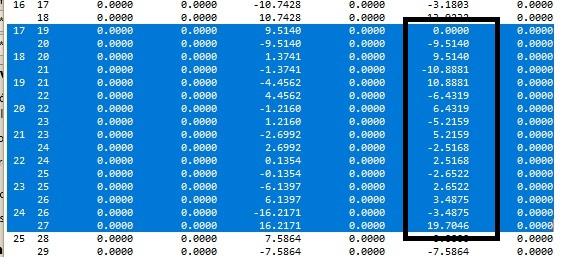
Valores obtidos MultCalcV10Urussanga com torção NULA


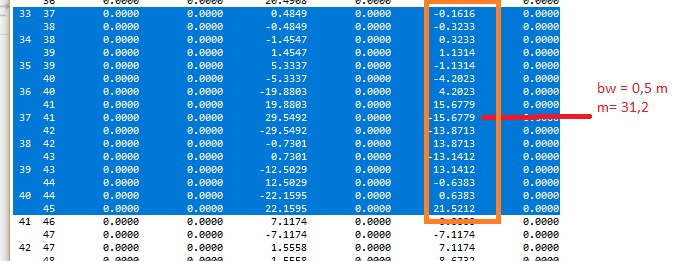
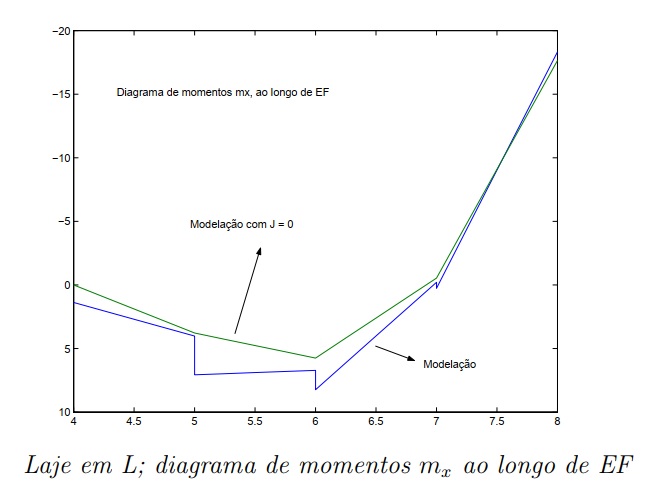
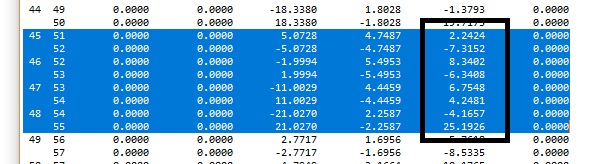
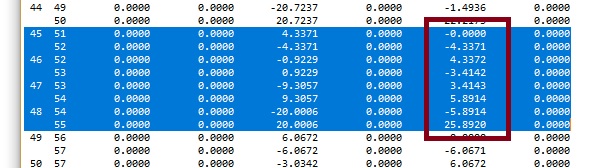
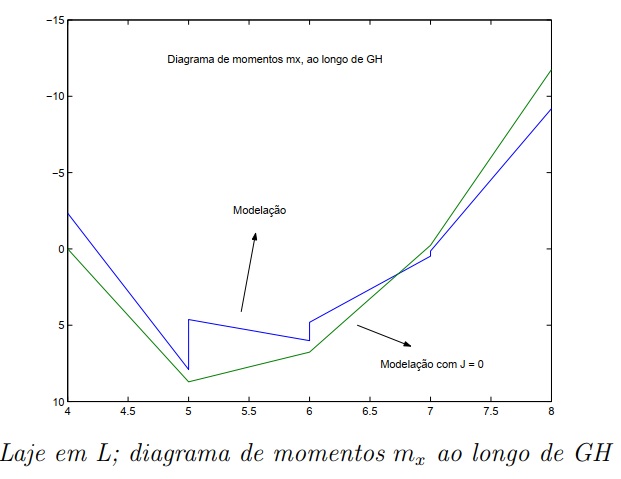
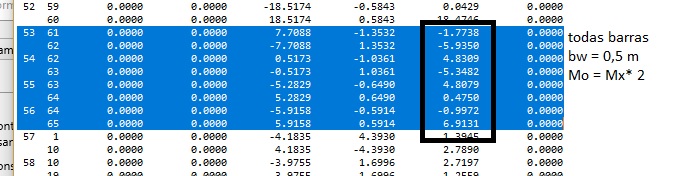
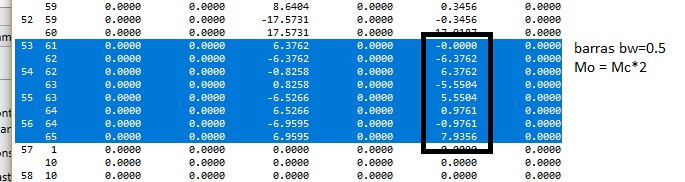
Os resultados obtidos pelo MultCalcV10-Urussanga com o algorítimo pórtico espacial 3d é praticamente igual ao do Obtido por Luíz Manuel Santos Castro em seu artigo. MODELAGEM DE LAJES COM ELEMENTOS DE GRELHA.