Para validação do modelo pórtico 3D e do Modelo de Grelha, calcularemos a seguinte laje simplesmente apoiada pelos dois algorítimos desenvolvidos no MultCalcV10-Urussanga.

Para ilustrar e validar as técnicas de modelação, considere-se a análise da laje simplesmente apoiada representada abaixo.
Considere-se que o carregamento é constituído por uma carga niformemente distribuída, q = 10 kN/m, aplicada em toda a laje. Considere-se ainda que esta possui uma espessura dada por h = 0, 20 m e que o material estrutural tem um módulo de elasticidade dado por E = 30500000 kN/m2 e um coeficiente de Poisson, ν = 0, 2.

Modelação

Adoptou-se um espaçamento unitáro h = 1, 0 m, na definição da grelha a utilizar.

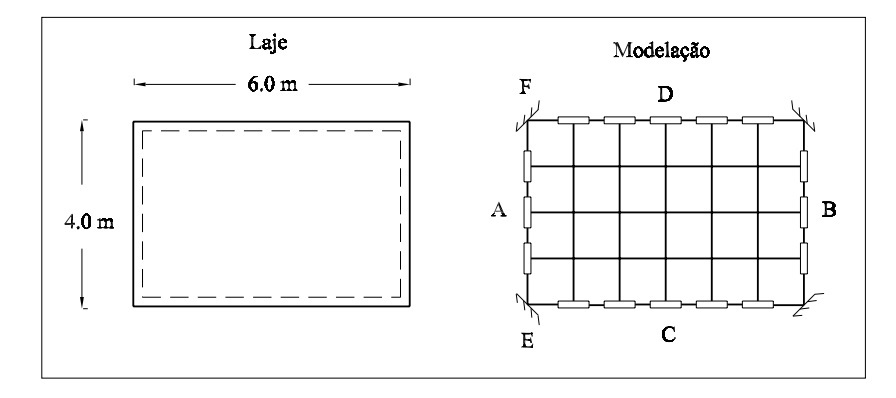
Na definição da rigidez aflexão e a torção existem dois tipos de barras a considerar: as barras que se encontram sobre os bordos da laje e as restantes. As primeiras modelam faixas de laje com uma largura de 0, 5 m, enquanto que as segundas modelam bandas com uma largura de 1 m.
Desta forma, e as propriedades a considerar na modelação são as seguintes:

Análise dos resultados

Na figura abaixo apresenta-se a aproximação obtida para o campo de momentos flectores my, ao longo do trecho CD. Nessa mesma figura representa-se a traço interrompido a correspondente solução exata. Esta última foi obtida com recurso a solução de Navier.

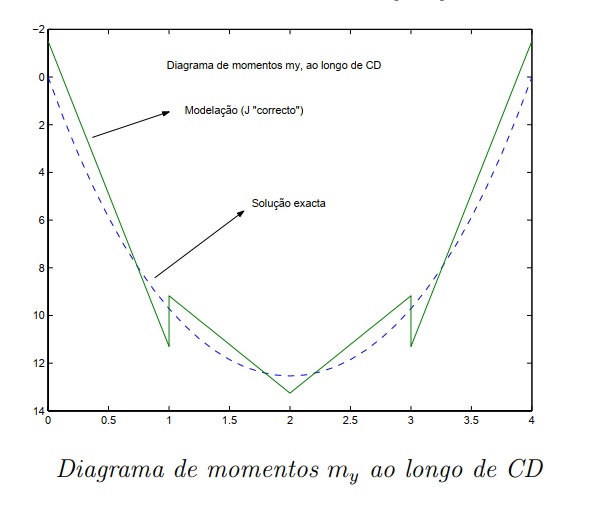
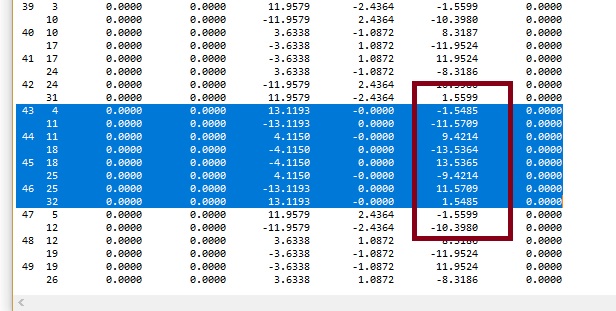
Verifica-se que a modelação considerada permite obter uma aproximação de muito boa qualidade para o campo de momentos em análise. Este facto ´e significativo, sobretudo se se tiver em consideração que ´e nesta direção (direção associada ao menor vão da laje) que se encontram os momentos flectores com maior valor absoluto, os quais irão condicionar
o dimensionamento da estrutura em estudo.
A análise do diagrama apresentado na acima permite ainda identificar algumas das características típicas dos resultados obtidos com recurso a esta técnica. Foi modelado os quatro cantos engastados e o restante do entorno como apoio cilíndrico.

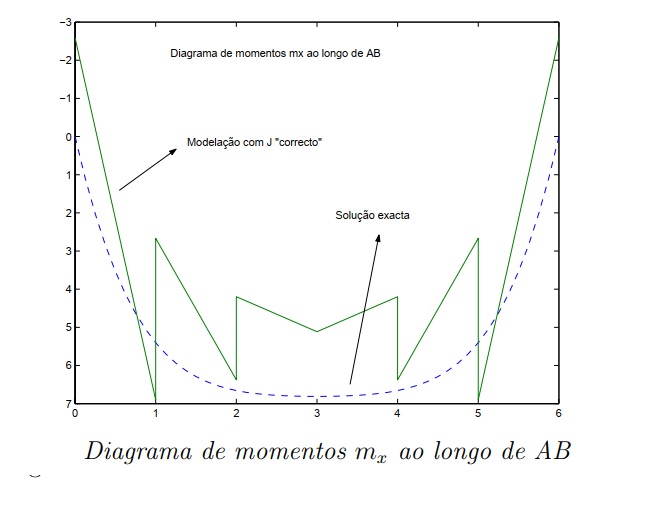
E´ também por existirem momentos torsores nas barras dispostas sobre os bordos da laje que os momentos flectores não se anulam em C e em D, como seria de esperar. Para conseguir garantir que os momentos sobre os bordos da laje se anulam, poderia ter sido considerado que o conjuntos de elementos de grelha que se situa no contorno tem um valor de J nulo. No entanto, esta escolha já não permite determinar qualquer aproximação para o campo de momentos torsores ao longo desses bordos, uma vez que quando se assume rigidez a torção nula para uma dada barra, ela passa apenas a “absorver” momentos flectores e esforços transversos.
Na acima representa-se o diagrama de momentos fletores mx, ao longo do trecho AB identificado na modelação. Tal como referido anteriormente, ao longo desta direção o valor máximo dos momentos é inferior ao que se regista na direção y, ao longo do trecho CD

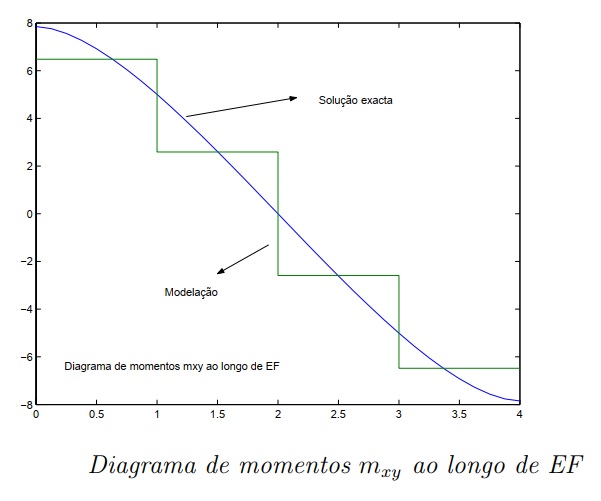
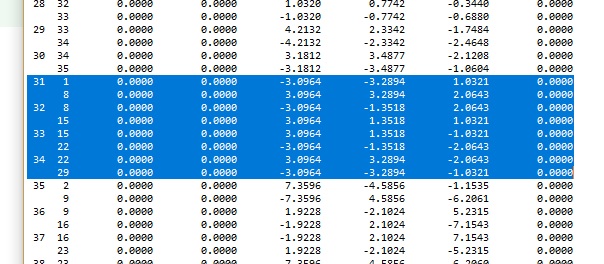
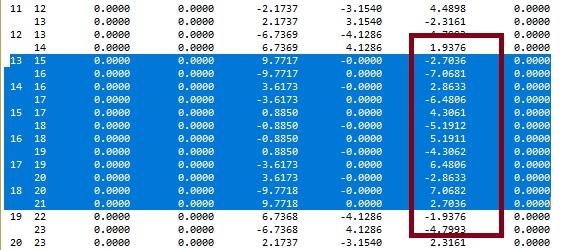
momentos torsores ao longo do bordo EF. Saliente-se que para se obter diagrama foi necessário multiplicar os valores dos correspondentes aos
momentos obtidos para os elementos de grelha existentes sobre o bordo, tendo em conta que na faixa de laje modelada tem uma espessura de apenas 0, 5 m.

O facto de se terem considerado apenas cargas nodais, faz com que o diagrama de momentos torsores aproximado obtido seja constante por traços. Interessante é verificar que esse valor constante ´e em cada um desses traços aproximadamente igual ao valor do diagrama exato no ponto médio do traço.

A aproximação conseguida para o campo de deslocamentos transversais, w, ao longo de AB, encontra-se representada na figura acima. E´ mais uma vez possível verificar uma muito boa concordância entre a solução aproximada obtida e a solução exata.

Os resultados obtidos pelo MultCalcV10-Urussanga com o algorítimo pórtico espacial 3d e com o algorítimo de Grelha 2d são exatamente iguais ao do Obtido por Luíz Manuel Santos Castro em seu artigo. MODELAGEM DE LAJES COM ELEMENTOS DE GRELHA. A única diferença entre os dois modelos pórtico espacial e Grelha é que no modelo de grelha o processamento como não poderia ser diferente é bem mais rápido. O primeiro envolve uma matriz com [6*nós][6*nós] dimensões e o segundo com [3*nós][ 3*nós] . Resultado igual foi obtido pelo estudo de Giovane Avancini FORMULAÇÃO DO MÉTODO DOS ELEMENTOS FINITOS PARA A ANÁLISE ELÁSTICA LINEAR DE VIGAS DE TIMOSHENKO (2015)