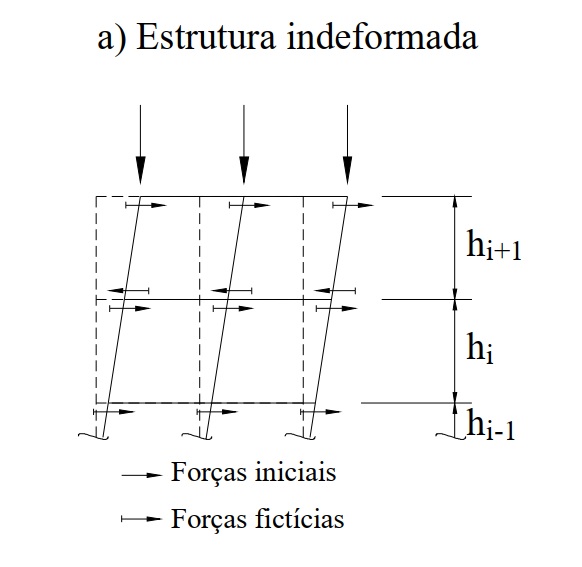
Devido à incidência das ações horizontais (normalmente devido aos ventos), os nós da estrutura sofrem deslocamentos, denominados efeitos de primeira ordem. Em virtude destes deslocamentos, as forças verticais atuantes nos nós da estrutura provocam o aparecimento de novos esforços (momentos), que por sua vez produzem novos deslocamentos, e assim sucessivamente até a posição final de equilíbrio. Estes esforços e deslocamentos adicionais podem ser obtidos pelo processo P-Delta , o qual consiste de uma análise através de iterações sucessivas nas quais as forças horizontais são incrementadas em cada iteração de forma a considerar o momento originado no respectivo pavimento devido aos deslocamentos e às
forças verticais atuantes nos nós. O processo P-Delta , ilustrado na Figura abaixo, será descrito a seguir:
1. Primeiramente, faz-se a análise de primeira ordem da estrutura, calculando-se os deslocamentos considerando a posição indeformada da estrutura. A partir da análise de primeira ordem, determinam-se os deslocamentos relativos entre os pavimentos;
2. Com os valores dos deslocamentos relativos entre os pavimentos, são obtidos os momentos proporcionais em virtude das ações das forças verticais atuantes nos nós;
3. Os momentos obtidos, então, são substituídos por binários equivalentes constituídos de forças horizontais, cujas resultantes são denominadas forças horizontais fictícias, cujos valores podem ser obtidos a partir da Expressão abaixo

As forças horizontais obtidas devem ser, então, adicionadas às forças horizontais atuantes nos nós da estrutura, e então é realizada a segunda iteração, e o processo é, então, repetido. Salienta-se que, a cada iteração, as forças horizontais modificadas resultam do somatório entre as forças horizontais iniciais e as forças horizontais
fictícias obtidas na referida iteração;
O processo deve ser repetido, segundo MacGregor (1988, apud LIMA, 2001), enquanto os deslocamentos de uma referida iteração excederem em mais de 5% da iteração anterior.