Neste capítulo estão apresentados exemplos numéricos com o intuito de consolidar os conceitos e de averiguar o algoritmo implementado e, consequentemente, o código gerado.
Faz-se a análise linear de diversas estruturas que tem como características ou modelo o funcionamento de viga, pilar, pórtico plano e pórtico tri-dimensional todos com ligações rígidas. Para estes tipos de estruturas são feitas também análises com não linearidade física e depois a não linearidade geométrica e finalmente em algumas é feito a análise de ligações semi-rígidas. O algorítimo do MultCalcV10-Urussanga resolve um pórtico tridimensional, portanto, todas as estruturas citadas podem ser resolvidas com o mesmo.
a)Análise de estrutura de vigas, com e sem consideração da não linearidade física
Modelo 1: Calcular os deslocamentos nodais, reações de apoio e esforçosos internos solicitantes da viga hiperestática apresentada na Figura A.1, sem consideração da fissuração, utilizando o programa MultCalcV10-Urussanga.
Dados:
1.Base da viga: 20 cm
2.Altura da viga: 20 cm
3.Módulo de elasticidade longitudinal (E) do concreto: 2,1 x 107 MPa.
4.Módulo de elasticidade transversal (G) do concreto: 6,0 x 106 Mpa.
5.Área da seção transversal: 0,04 m2.
6.Momento de inércia A flexão: 1,33 x 10-4 m4.
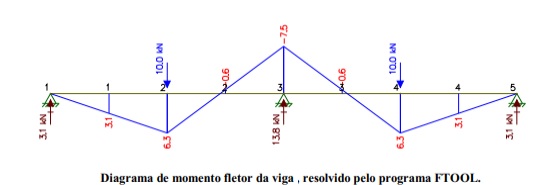
Figura A.1 – Viga hiperestática para análise estrutural utilizando o programa MultCalcV10-Urussanga.
Para a análise da referida estrutura, foi utilizada uma discretização bastante simples, que consiste da divisão da estrutura em apenas quatro trechos, os quais estão limitados pelos apoios e pelas cargas concentradas, conforme Figura A.2.
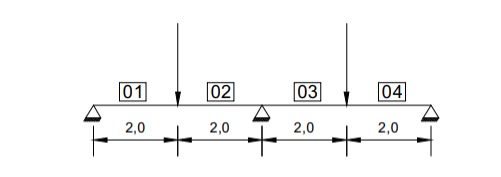
Figura A.2 – Discretização da estrutura,onde são apresentados os diversos elementos que a compoem.
Os dados fornecidos, assim como informações obtidas através da Figura A.1, podem ser organizados, formando-se o arquivo com as informações necessárias a utilização do programa MultCalcV10-Urussanga.
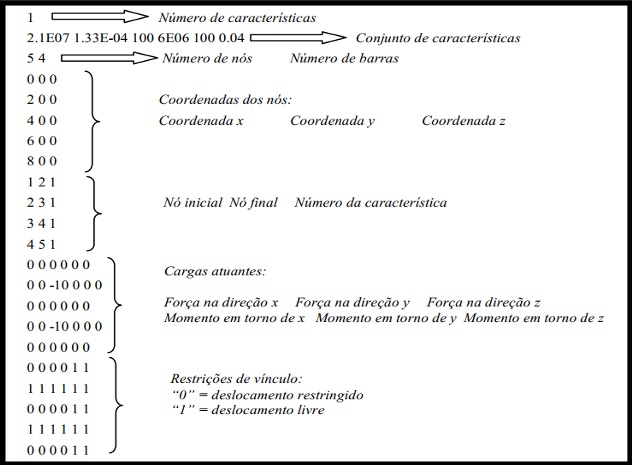
Após a análise da estrutura, obtém-se os resultados apresentados no Quadro abaixo.
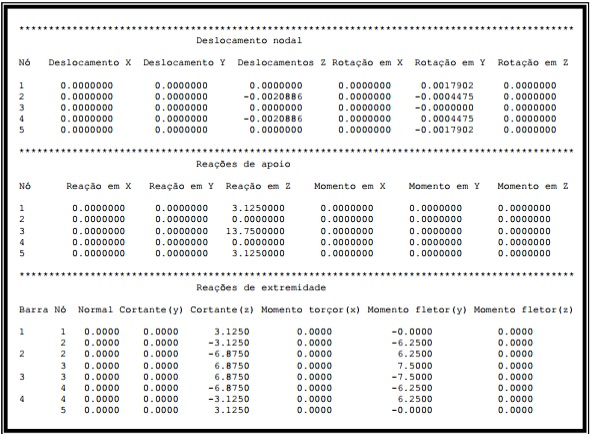
Com a finalidade de tornar válidos os resultados obtidos com a utilização do programa,a mesma estrutura foi analisada com o auxílio do programa FTOOL (MARTHA, 2006),obtendo-se os mesmos resultados, conforme é possível observar abaixo.

A orientação dos esforços de momento fletor e rotações pode ser obtida a partir da regra da mão direita, já bastante difundida entre os profissionais da àrea. Em suma, sinal negativo corresponde à rotação no sentido horário, enquanto que o sinal positivo corresponde à rotação no sentido anti-horário.
Modelo 2: Para a mesma viga do Modelo 1, calcular os deslocamentos nodais, os esforçosos internos solicitantes e as reações de vínculos, considerando-se os efeitos da fissuração. Os dados da estrutura correspondem aos fornecidos para o Modelo 1. acrescido destes adotar:
1. Momento de fissuração: 4,0 kN.m
2. Inércia no estádio I: 1,33 x 10-4 m4
3. Inércia no estádio II: 0,445 x 10-4 m4
Será efetuado utilizando a técnica de carregamento incremental, neste caso corespondendo a 10 incrementos de carga, de valor igual a Carga/10 obtém-se com o MultCalcV10-Urussanga, os resultados apresentados
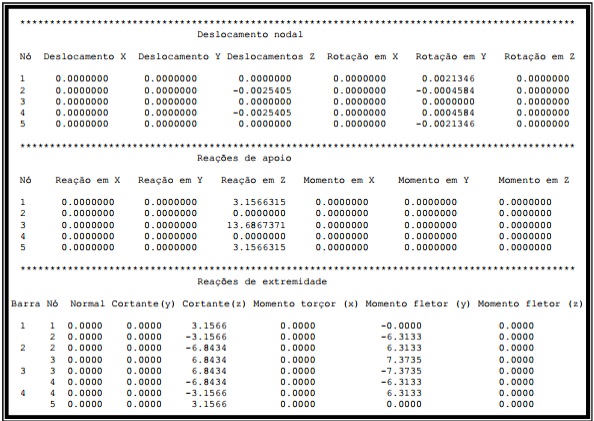
É fácil observar que, após a fissuração, o valor do momento negativo na região do apoio central diminuiu. Em contrapartida, o valor do momento positivo sofreu um ligeiro acréscimo. (valores destacados em vermelho na Figura abaixo), como esperado. Analogamente, os deslocamentos calculados considerando-se os efeitos da fissuração sofreram um acréscimo de aproximadamente 22%, o que também já era esperado.
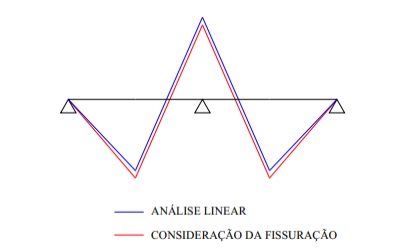
Diagrama de momento fletor para a estrutura dos Modelos 1 e 2, ou seja, sem análise não linear e com a análise não linear.
Conforme verificado no trabalho de Carvalho (1994), o aumento nos valores dos deslocamentos são bastante significativo, principalmente se comparado com os incrementos nos valores obtidos no momento fletor. Como exemplo, observemos os valores dos deslocamentos no nó 2 (ponto de aplicação da carga concentrada no primeiro tramo), obtidos a partir de uma análise linear e de uma análise não linear física, apresentados na Figura abaixo:
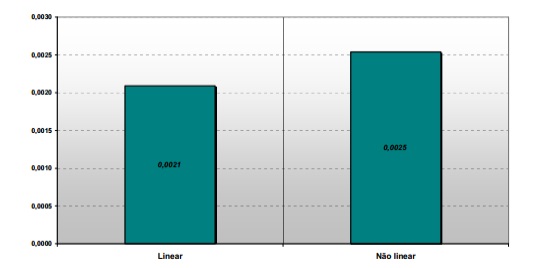
Valores dos deslocamentos para o nó 2 ponto de aplicação da carga no primeiro tramo.
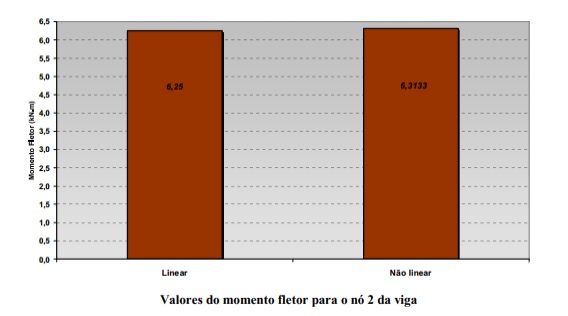
Em contrapartida, nota-se que a diferença entre os valores do momento fletor obtidos para no mesmo nó originado das análises linear e não linear física é consideravelmente menor em comparação com a diferença entre os valores dos deslocamentos, conforme Figura abaixo: